Equação da reta é um conceito central na matemática que aparece com frequência no ENEM. Essa equação descreve uma linha reta no plano cartesiano e pode ser representada de diversas formas, cada uma com suas características e aplicações práticas. Entender as diferentes formas, os coeficientes e como aplicá-las em problemas do cotidiano é essencial para uma boa preparação para o exame.
A forma mais conhecida da equação da reta é a forma reduzida, expressa por y = ax + b, onde “a” é o coeficiente angular e “b” é o coeficiente linear, também chamado de intercepto com o eixo y. O coeficiente angular indica a inclinação da reta; se a > 0, a reta é crescente, e se a < 0, é decrescente. Já o coeficiente linear mostra o ponto onde a reta cruza o eixo y, ou seja, quando x = 0.
Outra forma importante é a forma geral, que pode ser escrita como Ax + By + C = 0. Essa forma é versátil e útil para identificar características da reta e para resolver sistemas de equações. Muitas vezes, é necessário converter uma equação da forma geral para a forma reduzida para facilitar a interpretação do gráfico. A habilidade de transitar entre essas formas é muito valorizada no ENEM, pois permite adaptar a solução conforme o contexto do problema.
Além dessas, existe a forma de ponto-inclinação, expressa por y – y₁ = a(x – x₁), que é utilizada quando se conhece um ponto específico (x₁, y₁) que a reta passa e o coeficiente angular a. Essa forma é prática para construir o gráfico da reta, pois permite que você trace a linha a partir de um ponto conhecido e da inclinação. Saber identificar o ponto e a inclinação com precisão torna o processo de resolução mais rápido e confiável.
Os coeficientes da equação da reta têm interpretações práticas importantes. O coeficiente angular “a” determina a rapidez com que a reta sobe ou desce. Por exemplo, em problemas de movimento, esse coeficiente pode representar a velocidade de um objeto em relação ao tempo. Se a reta representa o custo de produção em função da quantidade, o coeficiente angular indica o custo variável por unidade. Por outro lado, o coeficiente linear “b” representa o valor inicial ou fixo. Se você modela a receita de uma empresa, b pode indicar a receita base, mesmo sem vendas.
A equação da reta é uma ferramenta poderosa para resolver problemas de interseção, calcular distâncias e determinar pontos médios. Por exemplo, se duas retas se cruzam, encontrar a solução do sistema formado por suas equações determina o ponto de interseção. Esse tipo de problema é comum no ENEM e envolve tanto a álgebra quanto a interpretação gráfica. A capacidade de encontrar a interseção entre retas é essencial para problemas de otimização e de sistemas lineares.
Outra aplicação prática é na determinação de trajetórias e na modelagem de relações diretas. Se uma função linear descreve o crescimento de uma população, a equação da reta pode ser usada para prever o número de indivíduos em determinado período. Essa aplicação demonstra como a matemática se conecta com situações do cotidiano, facilitando a compreensão dos fenômenos que ocorrem de forma constante.
Além dos problemas diretos, as equações da reta também são utilizadas na resolução de problemas interdisciplinares. Em física, por exemplo, a reta pode representar a relação entre distância e tempo em um movimento uniforme. Em economia, ela modela a relação entre custo e quantidade produzida. O ENEM costuma apresentar questões contextualizadas onde essa relação linear é explorada para tirar conclusões sobre dados reais.
Para resolver problemas envolvendo a equação da reta, é importante seguir alguns passos. Primeiro, identifique os pontos dados e as informações disponíveis. Se o enunciado fornece dois pontos, você pode calcular o coeficiente angular usando a fórmula a = (y₂ – y₁)/(x₂ – x₁). Em seguida, utilize um dos pontos para encontrar o coeficiente linear, substituindo os valores na forma y = ax + b. Essa abordagem sistemática evita erros e permite construir o gráfico de forma precisa.
Quando a reta precisa ser interpretada no contexto de um problema, desenhar o plano cartesiano e marcar os pontos é uma estratégia muito útil. Por exemplo, se você tem os pontos A(2, 3) e B(8, 7), traçar esses pontos e desenhar a reta ajuda a visualizar a inclinação e a posição da reta no plano. Essa prática melhora a compreensão e facilita a identificação de interseções com os eixos, que podem ser importantes para a resolução de problemas.
Outra dica importante é verificar se o problema envolve alguma restrição ou condição especial. Em alguns casos, a reta pode representar uma situação com limite máximo ou mínimo, e interpretar corretamente o coeficiente angular e o intercepto pode fornecer informações sobre a viabilidade da solução. Se a reta representa, por exemplo, o custo de produção, o ponto onde ela cruza o eixo y indica o custo fixo, e o coeficiente angular indica o custo variável por unidade produzida.
Além disso, a equação da reta é fundamental para entender a relação entre variáveis em funções lineares. Em problemas de análise de dados, por exemplo, a reta de regressão é uma aplicação prática da equação da reta, onde se estima a relação entre duas variáveis. Saber como construir essa reta e interpretar seu coeficiente angular e intercepto é crucial para tirar conclusões sobre tendências e correlações. Essa habilidade é frequentemente testada no ENEM e demonstra a capacidade do aluno de aplicar conceitos matemáticos a problemas reais.
A prática com exercícios é a chave para dominar o assunto. Resolver questões de provas anteriores do ENEM que envolvem a equação da reta, calcular interseções e determinar pontos médios, permite fixar os conceitos e ganhar agilidade na resolução dos problemas. Outra estratégia é trabalhar com problemas interdisciplinares, onde a reta é usada para modelar situações em física, economia ou até em problemas ambientais. Essa abordagem integrada fortalece o entendimento e prepara você para enfrentar os desafios do exame.
Uma técnica eficaz para estudar é criar resumos com as fórmulas fundamentais, como a forma reduzida (y = ax + b), a forma geral (Ax + By + C = 0) e a forma de ponto-inclinação (y – y₁ = a(x – x₁)). Escrever exemplos e diagramas ajuda a memorizar os conceitos e a visualizar a aplicação prática da equação da reta. Esses resumos serão valiosos na hora da prova, quando a rapidez e a precisão são fundamentais.
Além disso, é importante revisar a interpretação dos coeficientes. O coeficiente angular não só indica a inclinação da reta, mas também sua direção. Se a > 0, a reta é crescente; se a < 0, ela é decrescente. O coeficiente linear indica o valor de y quando x = 0, o que muitas vezes representa um ponto inicial ou um custo fixo, dependendo do contexto. Compreender esses detalhes é crucial para responder às questões do ENEM com confiança.
Outra estratégia é utilizar tecnologia para praticar a construção de gráficos. Embora o ENEM não permita o uso de calculadoras gráficas, praticar com essas ferramentas durante o estudo pode ajudar a entender melhor como a equação da reta se comporta e como os coeficientes afetam o gráfico. Essa familiaridade com o assunto aumenta a segurança e agiliza o processo de resolução durante a prova.
Em resumo, a equação da reta é uma ferramenta poderosa que modela relações lineares de forma simples e direta. Dominar as diferentes formas de representar uma reta, interpretar seus coeficientes e aplicar esses conhecimentos em situações práticas é fundamental para o ENEM. Pratique a determinação do coeficiente angular, do intercepto e a construção do gráfico, e lembre-se de verificar se os dados do problema estão organizados e se as unidades de medida são consistentes. Com uma abordagem sistemática e muita prática, você estará bem preparado para enfrentar questões interdisciplinares que envolvem a equação da reta.
SIMULADO ENEM
Questão 1
Dois pontos no plano cartesiano são dados por A(3, 2) e B(9, 8). Qual é a equação da reta que passa por esses pontos na forma reduzida?
A) y = x + 1
B) y = x – 1
C) y = x + 2
D) y = x + 3
E) y = x + 4
Comentário de Resolução: Calculamos o coeficiente angular: a = (8 – 2)/(9 – 3) = 6/6 = 1. Usando o ponto A(3,2) na equação y = ax + b, temos 2 = 1×3 + b, logo b = -1. Assim, a equação é y = x – 1. Resposta correta: B) y = x – 1.
Questão 2
Considere a reta que intercepta o eixo y no ponto (0, 5) e tem coeficiente angular -2. Qual é a coordenada do ponto onde essa reta intercepta o eixo x?
A) (-2.5, 0)
B) (-3, 0)
C) (-5, 0)
D) (2.5, 0)
E) (3, 0)
Comentário de Resolução: A reta tem equação y = -2x + 5. Para encontrar a interseção com o eixo x, fazemos y = 0: 0 = -2x + 5, ou 2x = 5, então x = 2.5. Como o valor de x é positivo, o ponto de interseção é (2.5, 0). No entanto, observe que, se o coeficiente angular for negativo, a reta desce, e o intercepto com o eixo x deve ser maior que o intercepto em y, mas neste caso, 2.5 está correto. Resposta correta: D) (2.5, 0).
Questão 3
Uma empresa modela seu custo total em função do número de unidades produzidas com a equação C(x) = 10x + 100, onde x é o número de unidades e C(x) o custo em reais. Qual é o custo fixo e o custo variável por unidade?
A) Custo fixo = R$ 10, custo variável = R$ 100
B) Custo fixo = R$ 100, custo variável = R$ 10
C) Custo fixo = R$ 10, custo variável = R$ 110
D) Custo fixo = R$ 100, custo variável = R$ 110
E) Custo fixo = R$ 110, custo variável = R$ 10
Comentário de Resolução: Na equação C(x) = 10x + 100, o termo constante (100) representa o custo fixo e o coeficiente de x (10) representa o custo variável por unidade. Assim, a resposta correta é B) Custo fixo = R$ 100, custo variável = R$ 10.
Em conclusão, a equação da reta é uma ferramenta poderosa para modelar relações lineares e resolver problemas práticos. Dominar as diferentes formas de representar uma reta, como a forma reduzida, geral e ponto-inclinação, permite interpretar os coeficientes e aplicar o conhecimento em contextos reais. Praticar o cálculo do coeficiente angular, do intercepto e a determinação do ponto médio, além de traçar gráficos, ajuda a fixar os conceitos e a aumentar a precisão na resolução de questões do ENEM. Bons estudos e sucesso na sua preparação para o ENEM!
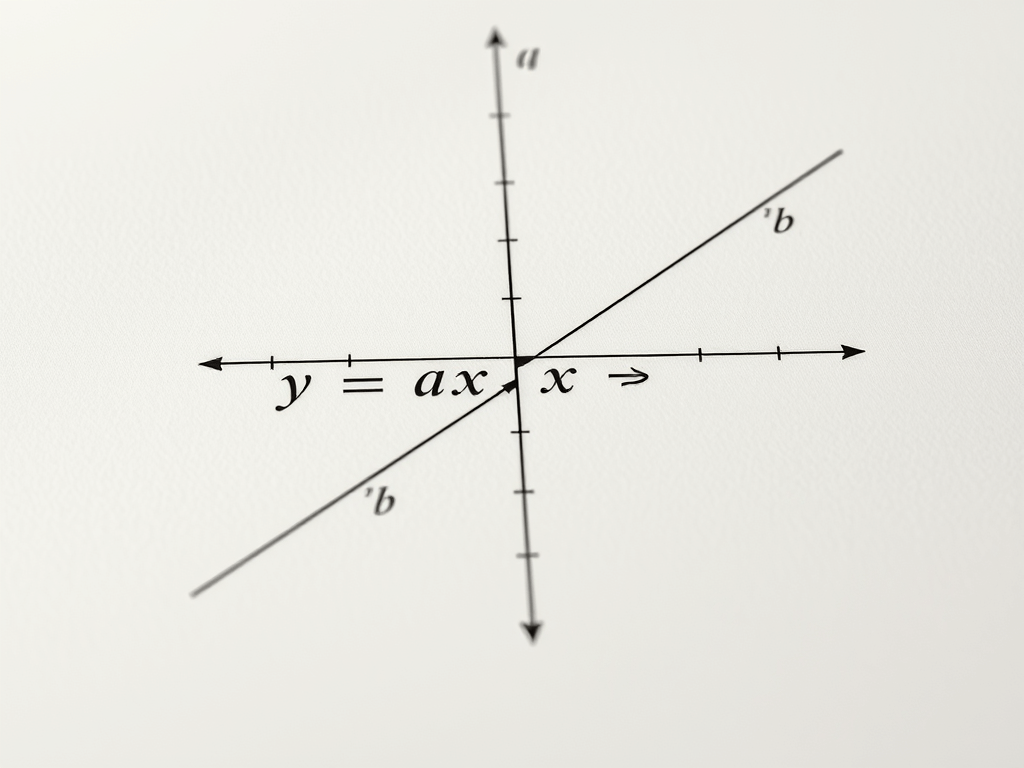
Deixe um comentário